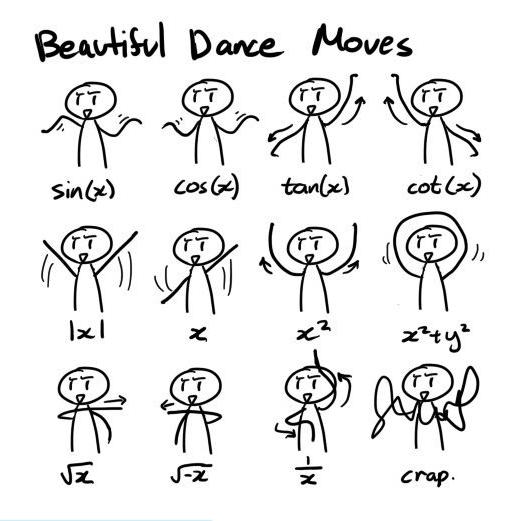萌娘百科欢迎您参与完善数学相关条目^∀^这里是计算与证明当道的理性世界.
可以从以下几个方面加以改进:
- 本条目属于“科普文改一下关键词”形式的“娘化”,不符合本站娘化要求,需要在用语萌化方面大幅度修改,以提高阅读兴趣
欢迎正在阅读这个条目的您协助
编辑本条目.编辑前请阅读
Wiki入门或
条目编辑规范,并查找相关资料.萌娘百科祝您在本站度过愉快的时光.
诚邀有志于完善数学相关条目的编辑们,加入萌娘百科数学组.QQ群:635986861(入群前请注明萌百ID).

|
| 基本资料
|
| 本名
|
函数
|
| 别号
|
含树娘
|
| 萌点
|
清纯、内涵、吃货
|
| 出身地区
|
地球
|
| 活动范围
|
全球
|
| 所属团体
|
数学娘
|
| 亲属或相关人
|
| 家族的大姐大兼百合:数学娘、朋友兼百合:代数娘
|
函数娘是各类函数的拟人化萌娘。
函数娘资料
清纯可爱而内涵的萌娘。
娘如其名,性格内向,仿佛总有心事一般。
以下是函數最一般的定義
警告!前方侦测到
不明级别的高能反应!
请非战斗人员迅速撤离!
|
|
$\displaystyle A,B$都是集合,$f\subseteq A\times B$滿足
- $(\forall a\in A)(\exists! b)\{(b \in B)\wedge[(a,b)\in f]\}$
稱$\displaystyle f$為從$\displaystyle A$映射到$\displaystyle B$的函數(function),以符號$f:A \rightarrow B $表示。
其中$\displaystyle A$被稱為定義域(domain),$\displaystyle B$被稱為對應域(codomain)。
Would you like to know more?還不快自己去查一階邏輯和公理化集合論
|
函數娘就像是商店的看板娘,親切的向顧客提醒擺在商店裡的東西都有不二價。函數的定義口語版
虽然和数学娘相似:拥有高超的计算能力,处理任何事物都理性客观。但做事不死板,喜爱绘画,舞蹈。虽然说只有小部分函数娘是能被画出来的
有吃货属性,故也有人称其含树娘。同时和数学娘、代数娘是百合关系
如果沒有特別說明,本篇函數的定義域和對應域都會是實數系$\mathbb{R}$。
根据编辑者的所见所闻,函数娘有如下几种形态
常数/常值函数形态
以複數系為定義域,自攻自受。
解析式$y = a$,是函数娘最为常见的形态(一条平行于 $x$ 轴的直线),贫乳,一般不会被人提及。
一次函数形态
以複數系為定義域,自攻自受。解析式$y = kx + b(k ≠ 0)$,也是函数娘最为常见的形态(一条不平行于 $x$ 轴的直线),但这时候新房45度的函数娘能给人一种清新可爱的感觉(这是为什么捏?)。
当$b = 0$时,成为正比例函数,解析式 $y = kx$ ,是一条过原点的倾斜直线。
当$b ≠ 0$时,函数会和坐标轴拼刺刀形成暧昧的交♂点。与$y$轴的交♂点为$($$0$$, b)$,与$x$轴的交♂点为$(-k/b, 0)$。
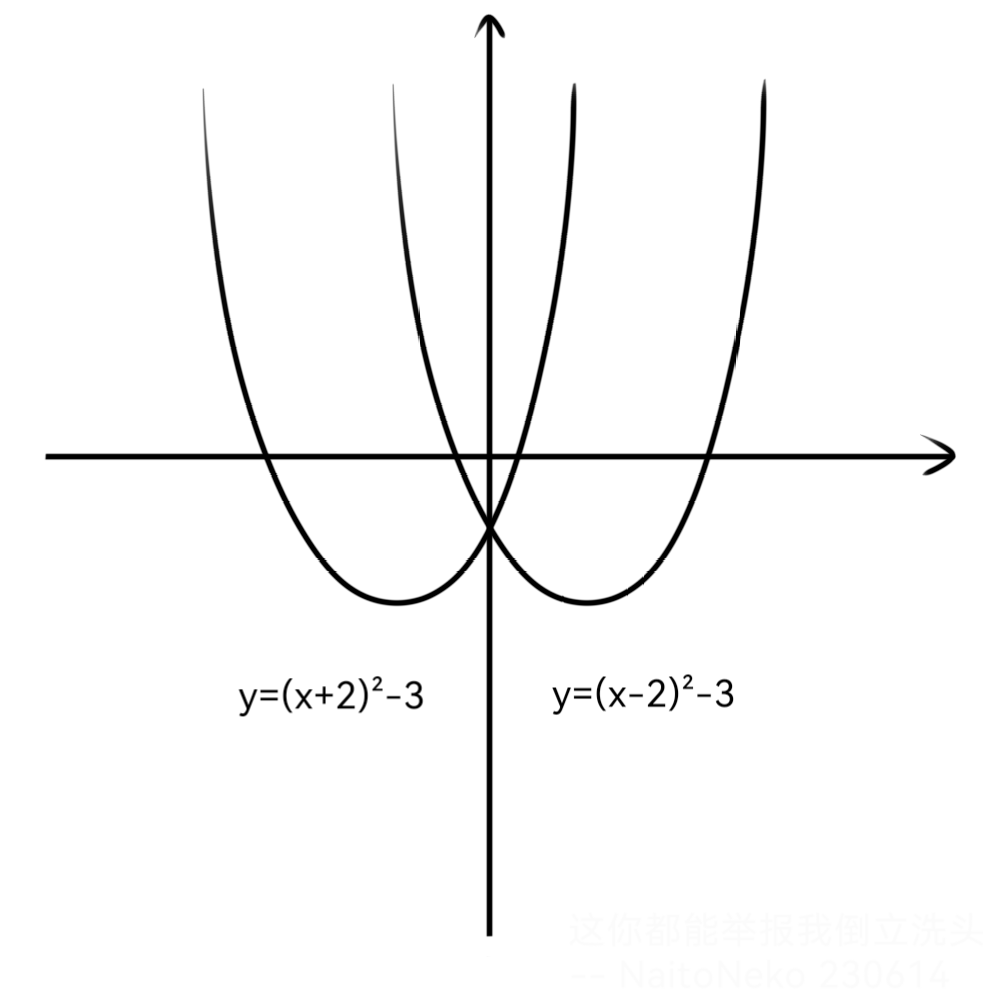
二次函数形态
解析式$y = ax^2 + bx + c(a \neq 0)$ ,是函数娘较为常见的形态(一条抛物线),这时候的函数娘就是大家俗知的吃货啦,没看见她张大了嘴巴准备大吃一顿么?据编辑者所知, $a$ 的绝对值越小,函数娘的嘴巴张的就越大呢!所以这时的函数娘经常被大家YY
反比例函数形态
解析式$y = \frac{k}{x}(k \neq 0)$ ,是函数娘练习舞蹈时的形态(双曲线),这时得函数娘的舞姿很动人(看看后面的函数舞你就知道了),这和她平常给人的清新感大不一样,是一种不太常见的形态。
其它形态
| 其他较为常见的函数娘形态
|
初等函数
初等函数是由基本运算 (例如, 加减乘除、指数、对数) 构成的函数,函数娘从小就会初等函数.
代数函数
- 代数函数: 能够表示为多项式方程的函数
- 多项式: 为多个单项式之和,能够表示为变量的加减和乘,也就是
- $\displaystyle y=\sum_{i=0}^{n}a_k x^k$
- 线性函数: 一次多项式, 图像为直线
- $y=ax+b$
- 二次函数: 二次多项式, 图像为抛物线
- $y=ax^2+bx+c$
- 以$x$非零項的最高次方命名為$n$次函數,以此類推。零次函數特稱為常數函數。
- 有理函数: 两个多项式函数的比,也就是如果有兩個多項式$P(x)$、$Q(x)$,且
- $A = \{x\in\mathbb{R}\,|\,Q(x)\neq 0\}$
- 則有理函數$f:A\to\mathbb{R}$的形式為
- $\displaystyle f(x)=\frac{P(x)}{Q(x)}$
- 若$P(x)$為常數函數,$f$特稱為分式函数。
- 开方
- $\displaystyle y=x^{\frac{1}{n}}$
- 一般簡寫為$\displaystyle y = \sqrt[n]{x}$,最普通的就是$n=2$,也就是平方根($y = \sqrt{x}$)
基本超越函数
非代数函数即为超越函数.
- 指数函数: $y=a^x$(a为非1正数) 当0<a<1时递减,a>1时递增
- 双曲函数: 形式上相似于三角函数.
- 对数: $y=\log_ax$(a为非1正数)为以a为底对数,指数函数的反函数; 用于求解指数方程.
- 自然对数$y=\ln x$为以e为底对数
- 常用对数$y=\lg x$为以10为底对数
- 二进对数$y=\log_2x$为以2为底对数
- 不定对数
- 幂函数:$y=x^k$
- 周期函数
- 三角函数: 正弦, 余弦, 正切等.; 主要用于几何学和描述周期现象. 参阅古德曼函数.
- 锯齿波
- 方波函数
- 三角波
特殊函数
- 基本特殊函数
- $1_{A}(x) = \begin{cases}\begin{matrix} 1 & (x\in A) \\ 0 & (x \not\in A) \end{matrix}\end{cases}$
- 若以$\mathbb{Q}$表示有理數系,$1_{\mathbb{Q}}(x)$特稱为狄利克雷函数。
- 取整函数:
- $[x]=\max \,\{n\in \mathbb {Z} \mid n\leq x\}$
- 单位阶跃函数:
- $H(t) = \begin{cases}\begin{matrix} 0 & (t<0) \\ 1 & (t\geq 0) \end{matrix}\end{cases}$
- 符号函数:
- $\text{sgn}(t) = \begin{cases}\begin{matrix} 1 & (t>0) \\ 0 & (t=0) \\ -1 & (t<0)\end{matrix}\end{cases}$
- 绝对值函数: 为某点到原点的距离.\
- 狄拉克泛函(俗稱的狄拉克函數):
- $C^{\infty}(\mathbb{R})$代表所有定義域在$\mathbb{R}$,但
- $\operatorname{supp} f=\{r\in \mathbb{R}\,|\,f(r)\neq 0\}$
- 是緊緻的(這個術語的意思留當課後習題),且可無限微分的實數函數$f$的集合(
俗稱定義於$\mathbb{R}$且有緊支持的光滑函數空間)
- 所謂的狄拉克泛函擎天柱函数,就是$\delta:C^{\infty}(\mathbb{R})\to\mathbb{R}$滿足
$$\delta[f] = f(0)$$
|
函数舞
由函数娘独创的一套舞蹈,曾在中学生阶层中疯传,众学生纷纷表示自从学习了此舞蹈后,与函数娘亲近了许多。
下图是函数舞的教程
此图中$\sin{x}$ 的舞蹈动作做反了←你不把身体当y轴的话,就可以认为它没啥问题.jpg
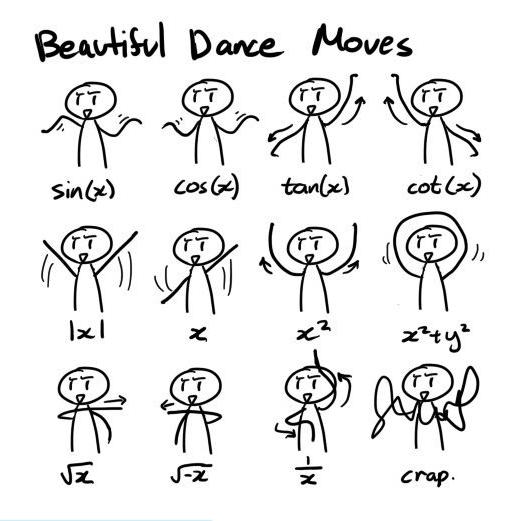
| 学科拟人(学科娘大家族)——各种学科的拟人化萌娘 |
|---|
| | 理学类 | | | | 工学类 | | | | 农学类 | | | | 医学类 | | | | 哲学类 | | | | 管理学类 | | | | 经济学类 | | | | 语言文学类 | | | | 艺术学类 | | | | 法学类 | | | | 教育学类 | | | | 历史学类 | | | | 军事学类 | |
|
| 数学相关条目 |
|---|
| | 数学萌化 | | | | ACGN中的数学要素 | | 数学要素总览列表 | | | | 数学相关音乐 | | | | 数学相关作品 | | | | 数学相关用语 | | | | 数学相关角色 | | | | 数学相关萌属性 | |
|
|
外部链接

维基百科
提示您 | 关于函数娘,
在自由的百科全书维基百科上
有相关条目。
请参阅:函数 |
此頁面正在運行MathJax