ACGN作品中的数学要素列表
跳到导航
跳到搜索
在不少ACGN作品（尤其是校园相关题材的作品）中，有时会出现与数学相关的要素。本条目旨在以列表方式，收集并记录这类数学要素。
- 萌娘百科不提供数学建议。若对任何页面上的数学概念与证明等有疑问，请参考正规的数学书籍与百科。
- 欢迎您对条目中可能的错误进行更正，并改善条目中的图片排版。
| 编辑注意事项 |
|---|
|
警告！前方侦测到
大量不同难度数学级别的高能反应！
请非战斗人员迅速撤离！
大量不同难度数学级别的高能反应！
请非战斗人员迅速撤离！
列表概览
下表概括了目前页面中含有的内容：
| 番剧年份 | 番剧名 | 集数 | 数学知识点 | 备注 |
|---|---|---|---|---|
| 2011 | 魔法少女小圆 | 第1、10集 | 中学代数/数论 | - |
| 2014 | 寄生兽 | 第3集 | 中学代数 | - |
| 2015 | 暗杀教室 | 第2季第12集 | 立体几何/晶体学 | - |
| 2017 | One Room | 第1季第2集、第3季第8集 | 中学代数/几何/概率 | - |
| 2018 | 寄宿学校的朱丽叶 | 第3、4集 | 代数 | - |
| 2018 | Slow Start | 第6集 | 微积分 | - |
| 2018 | 莉兹与青鸟 | N/A | 数论 | - |
| 2018 | DARLING in the FRANXX | 第13集 | 中学代数/数论 | - |
| 2021 | 黄金拼图 Thank you!! | N/A | 平面几何 | - |
| 2023 | 别当欧尼酱了！ | 第7集 | 中学代数/几何 | - |
| 2009 | 轻音少女 | 第1季第3集 | 因式分解 | - |
| 2010 | 笨蛋、测验、召唤兽 | 第1季第1集，后续尚未考证 | - | - |
| 2014 | 一周的朋友。 | 第1集等 | 三角函数 | - |
| 2020 | 理科生坠入情网，故尝试证明。 | 全集 | 什么都有 | - |
| 2022 | 欢迎来到实力至上主义的教室 | 第2季第9集 | 中学代数/概率 | - |
| 2004 | GANTZ | 第1集 | - | - |
| 2006 | 樱兰高校男公关部 | - | - | - |
| 2006 | 穿越时空的少女 | N/A | - | - |
| 2010 | 圣诞之吻 | - | - | - |
| 2011 | 偶像大师 | 第1集 | - | - |
| 2011 | 日常 | 第3集 | - | - |
| 2012 | 冰菓 | - | - | - |
| 2012 | 邻座的怪同学 | - | - | - |
| 2013 | 魔法少女伊莉雅 | - | - | - |
| 2013 | Lovelive! | - | 因式分解、实数等 | 游戏中东条希的卡牌“一直都这样下去……”背景中亦有出现数学要素 |
| 2015 | 关于我被绑架到大小姐学校当庶民样本这件事 | - | - | - |
| 2016 | 时间旅行少女 | 第1集等 | - | - |
| 2017 | 徒然喜欢你 | - | - | - |
| 2017 | 珈百璃的堕落 | 第12集 | - | - |
| 2018 | 终将成为你 | 第5集 | 因式分解 | - |
| 2018 | 擅长捉弄人的高木同学 | - | - | - |
| 2018 | 杀戮的天使 | - | - | - |
| 2018 | ISLAND | - | - | - |
| 2019 | 五等分的新娘 | - | - | - |
| 2019 | 我们真的学不来 | - | - | - |
| 2019 | 约定的梦幻岛 | - | - | - |
| 2022 | 吹响！上低音号 | 第2季第6集 | 因式分解 | - |
| 2015 | Charlotte | 第1集 | 中学代数 | 第1集中间出现的试卷中，含有二次函数的一部分图示，但因试卷过于模糊，无法辨别上面的文字 |
A
《暗杀教室》
动画第2季第12话中，赤羽业与浅野学秀所面对的数学压轴题，是一道求体心立方体体积的题目。该题很明显超出了作品设定中，初中数学的范围。
|
| 翻译后的题干 |
|---|
|
右图中，边长为$a$的正方体呈周期型排列，这种在正方体的各顶点及中心各有一个原子的晶体构造被称为体心立方体。Na、K等碱金属多为这种结构。
在一个体心立方体中，以某一个原子$A_0$为中心，令空间内离$A_0$最近的所有点（此处“最近”意为与$A_0$的距离小于与任意其他原子的距离）组成的多面体为$D_0$，求$D_0$的体积。
|
这道题背后的理论，来源于化学中的Wigner-seitz原胞体积（类似的晶体结构问题，也是化学中与数学联系最紧密的部分之一）。对于立方体型排列的原子，这是一个14面体的体积。
| 浅野学秀的思路（立方体切割） |
|---|
|
浅野学秀的思路是，将中心的多面体视为一个立方体砍去周围八个角，并计算每个角上砍去部分的体积。这种思路虽然可行，但由于周围八个角本身也是很复杂的多面体，求体积的计算量较大，由于剩余时间过短没有解完这道题。 实际上，在网络上，并未查阅到以这种思路解题的可能性。如果要使用切割的方式解决问题的话，更好的方式是将原多面体想象成、一个正八面体切除六个角上的正四面体后的结果。[1] |
| 赤羽业的思路（对称性） | ||
|---|---|---|
|
注意到每个原子$A$对应的空间$D$组成了全空间，而各个原子的地位又是相同的，即每个原子对应的空间的大小为单位体积内原子个数的倒数。在每个立方体中，有一个体心原子和八个顶点原子。但每个顶点原子分属于八个立方体，所以每个顶点原子实际上只算$\frac{1}{8}$个。因而，在$a^{3}$的空间中有2个原子，每个原子的对应的空间大小为$\frac{a^{3}}{2}$。
|
B
《笨蛋、测验、召唤兽》
黑板上的数字
第一季第1集的10分钟左右，坂本雄二与吉井明久发表演说时，背景中的黑板上写满了数字。仔细观察可发现其为数学常数π的小数点后前230位。为什么一群笨蛋的班里会有人写π的小数点后数字啊……
|
剧中的数学试卷
第一季第1集的17至20分钟，角色姬路瑞希和岛田美波在参加补习测试时，剧中出现了两人使用的数学试卷。其中包含因式分解、因式展开，二次方程的解的性质的问题。
|
翻译后的题目如下：
岛田美波试卷第一题的8-11小问
| 题目 |
|---|
|
展开下列算式： （8）$(2x-1)\left(4 x^{2}+2 x+1\right)$
（9）$(2 x+3 y)\left(4 x^{2}-6 x y+9 y^{2}\right)$
（10）$(x-1)\left(x^{2}+x+1\right)\left(x^{6}+x^{3}+1\right)$
（11）$\left(x^{2}-y^{2}\right)\left(x^{2}+x y+y^{2}\right)\left(x^{2}-x y+y^{2}\right)$
|
| 官方解答 |
|---|
|
（8）$\begin{aligned}&(2x-1)\left(4 x^{2}+2 x+1\right)\\ &=(2 x)^{3}-13=8 x^{3}-1\end{aligned}$
（9）$\begin{aligned}&(2 x+3 y)\left(4 x^{2}-6 x y+9 y^{2}\right)\\ &=(2 x)^{3}+(3 y)^{3}=8 x^{3}+27 y^{3}\end{aligned}$
（10）$\begin{aligned}&(x-1)\left(x^{2}+x+1\right)\left(x^{6}+x^{3}+1\right)\\ &=\left(x^{3}\right)^{3}-1=x^{4}-1\end{aligned}$
（11）$\begin{aligned}&\left(x^{2}-y^{2}\right)\left(x^{2}+x y+y^{2}\right)\left(x^{2}-x y+y^{2}\right)\\&=\left(x^{3}-y^{3}\right)\left(x^{3}+y^{3}\right)=x^{6}-y^{6}\end{aligned}$
|
岛田美波试卷第二题的1-4小问
| 题目 |
|---|
|
简化下列算式： （1）$(\sqrt{3}+\sqrt{2})^{2}+(\sqrt{3}-\sqrt{2})^{2}$
（2）$(\sqrt{6}+1)^{2}-2(\sqrt{6}+1)-3 $
（3）$\sqrt{27}+\sqrt{12}-\sqrt{48}$
（4）$\sqrt{(-3)^{2}}+\sqrt{(3-\pi)^{2}}$
|
| 官方解答 |
|---|
|
（1）$\begin{aligned}&(\sqrt{3}+\sqrt{2})^{2}+(\sqrt{3}-\sqrt{2})^{2}\\&=(3+2 \sqrt{6}+2)+(3-2 \sqrt{6}-2)=10\end{aligned}$
（2）$\begin{aligned}&(\sqrt{6}+1)^{2}-2(\sqrt{6}+1)-3 \\&=(6+2 \sqrt{6}+1)-2 \sqrt{6}-2-3=2 \end{aligned}$
（3）$\begin{aligned}&\sqrt{27}+\sqrt{12}-\sqrt{48}\\&=3 \sqrt{3}+2 \sqrt{3}-4 \sqrt{3}=\sqrt{3}\end{aligned}$
（4）$\begin{aligned}&\sqrt{(-3)^{2}}+\sqrt{(3-\pi)^{2}}\\&=-(-3)-(3-\pi)=\pi\end{aligned}$
|
岛田美波试卷第三题
| 题目 |
|---|
|
（本题部分题干内容缺失，红色字体部分为对缺失内容的补充） 令二次方程$x^2+kx+1=0$的解为$\alpha$和$\beta$，其中$k$为常数。求解以下问题：
（1）若$\alpha$和$\beta$均为实数，求$k$的范围。
（2）众所周知，如果$\alpha>0$，$\beta>0$，则可得$\alpha+\beta>0$和$\alpha\beta>0$。证明其逆命题：若$\alpha+\beta>0$和$\alpha\beta>0$，则$\alpha>0$，$\beta>0$。
（3）根据（2）中的结论，若$\alpha$和$\beta$均为正实数，求$k$的范围。
|
|
（1）根据二次方程解公式，可知我们需要$k^2-4\geq 0$，即$k\geq 2$或$k\leq -2$。
（2）若$\alpha\beta>0$，则它们必定同为正或同为负。因为$\alpha+\beta>0$，所以它们只可能是同为正。
（3）根据二次方程解的性质，可知$\alpha+\beta=-k$，$\alpha\beta=1$。因此我们需要满足$k<0$。结合（1），所求范围为$k\leq -2$。
|
姬路瑞希试卷第一题
| 题目 |
|---|
|
因式分解： （1）$a^{2} b+a b^{2}+a+b-a b-1$
（2）$(x+y)(y+z)(z+x)+x y z$
（3）$x\left(y^{2}-z^{2}\right)+y\left(z^{2}-x^{2}\right)+z\left(x^{2}-y^{2}\right)$
（4）$x^{3}+y^{3}+z^{3}-3 x y z$
（5）$x^{4}-13 x^{2}+36$
（6）$\left(x^{2}+x-5\right)\left(x^{2}+x-7\right)+1$
（7）$(a+b+c+1)(a+1)+b c$
（8）$4 x^{2}-4 x y+y^{2}-6 x+3 y-10$
|
| 解答 |
|---|
|
(1)-(6)为官方解答，其中（2）中补全了右侧缺失的部分；(7)-(8)为非官方解答。 （1）$\begin{aligned}&a^{2} b+a b^{2}+a+b-a b-1\\&=b a^{2}+\left(b^{2}-b+1\right) a+b-1\\&=(a b+1)(a+b-1) \end{aligned}$
（2）$\begin{aligned}&(x+y)(y+z)(z+x)+x y z\\&=(y+z) x^{2}+\left(y^{2}+3 y z+z^{2}\right) x+y z(y+z)\\&=(x+y+z)^2\end{aligned}$
（3）$\begin{aligned}&x\left(y^{2}-z^{2}\right)+y\left(z^{2}-x^{2}\right)+z\left(x^{2}-y^{2}\right)\\&=-(y-z)(x-y)(x-z)=(x-y)(y-z)(z-x)\end{aligned}$
（4）$\begin{aligned}&x^{3}+y^{3}+z^{3}-3 x y z\\&=(x+y+z)\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)\end{aligned}$
（5）$\begin{aligned}&x^{4}-13 x^{2}+36\\&=(x+2)(x-2)(x+3)(x-3)\end{aligned}$
（6）$\begin{aligned}&\left(x^{2}+x-5\right)\left(x^{2}+x-7\right)+1\\&=\left(x^{2}+x-6\right)^{2}=(x+3)^{2}(x-2)^{2}\end{aligned}$
（7）$\begin{aligned}&(a+b+c+1)(a+1)+b c\\&=(a+1)^{2}+(b+c)(a+1)+bc\\&=(a+1+b)(a+1+c)\end{aligned}$
（8）$\begin{aligned}&4 x^{2}-4 x y+y^{2}-6 x+3 y-10\\&=(2x-y)^{2}-3(2x-y)-10\\&=(2x-y-5)(2x-y+2)\end{aligned}$
|
《别当欧尼酱了！》
动画第7集4分18秒，绪山真寻在学校考试时发下的数学试卷。其中涉及到追及问题和反比例函数与几何的问题。
|
翻译后的题目如下：
试卷第7题
| 题目 |
|---|
|
哥哥从$1500\mathrm m$外的书店回家，妹妹在哥哥出发$7$分钟后沿相同道路追赶哥哥。哥哥和妹妹分别以每分钟$60\mathrm m$、每分钟$80\mathrm m$的速度前进。妹妹在出发后$x$分钟追上了哥哥。解答下列问题：
(1) 用含有$x$的式子表示妹妹追上哥哥前走过的路程。
(2) 列出方程并求出妹妹出发后多久追上哥哥。
|
试卷第8题
| 题目 |
|---|
|
如右图所示，在平面直角坐标系$xOy$中，反比例函数$y=\cfrac{24}{x}$的图象上有一点$B$，与$y$轴上的点$A$和$x$轴上的点$C$以及原点$O$围成一矩形$OABC$。该坐标系单位长度为$1\mathrm{cm}$。解答下列问题：
(1) 求矩形$OABC$的面积。
(2) 若点$C$坐标为$(6,0)$，求点$A$坐标。
(3) 若$OA$的长度为$3\mathrm{cm}$，求$OC$的长度。
|
| 因为小寻子认为试卷太简单结果睡着了导致答案空缺，以下给出非官方解答 |
|---|
|
第7题 $(1)80x.$
$(2)$由题意,得$60x+60·7=80x$,解得$x=21$.
第8题 $(1)$设点$B(b,\frac{24}{b})$,则$OA=\frac{24}{b}(\mathrm{cm})$,$OC=b(\mathrm{cm})$.所以$S_{矩形OABC}=b\times\frac{24}{b}=24(\mathrm{cm^2})$.
$(2)$令$x=6$,则$y=\frac{24}{6}=4$,即$A(0,4)$.
$(3)$令$y=3$,得$3=\frac{24}{x}$,解得$x=8$,即$OC=8\mathrm{cm}$.
|
D
《DARLING in the FRANXX》
动画第13集开头，课堂黑板上出现了大量图形与数字。大部分内容疑似为智商测试题，但其中也夹杂着一些难度不一的数学公式，可辨认的要素包含如下：
- 中间黑板：左下角的杨辉/帕斯卡三角，右侧的三角函数的周期性。
- 下方黑板：整块黑板记录了大量斐波那契数列的性质、以及斐波那契螺旋的图片。
此外，最上侧黑板的左侧、以及与下方黑板的左上角，还记录了一些物理学中，圆周运动以及匀加速运动相关的计算公式。
记载的数学内容一般理解为高中内容。虽然番剧中上课学生从外表上看类似初中生，但因为番剧的科幻元素，无法确定学生的生理/心理年龄，因此也无法考证难度是否合理。
|
E
F
G
H
《欢迎来到实力至上主义的教室》
动画第2季第9集16分17秒，
此处仅给出第2、3题的翻译：
第2题
| 题目 |
|---|
|
将字母$\mathrm{a, a, b, c, d}$横向排成一行。
(1) 一共有多少种排列方式？
(2) 出现字母组合“$\mathrm{ab}$”的排列方式有多少种？
(3) 字母$\mathrm{a}$和$\mathrm{b}$相邻的排列方式有多少种？
|
第3题
| 题目 |
|---|
|
算出所有满足方程$\sqrt{4a^2 - 4a + 1} + | a + 4 | = a + 7$的$a$的值。
|
《黄金拼图 Thank you!!》
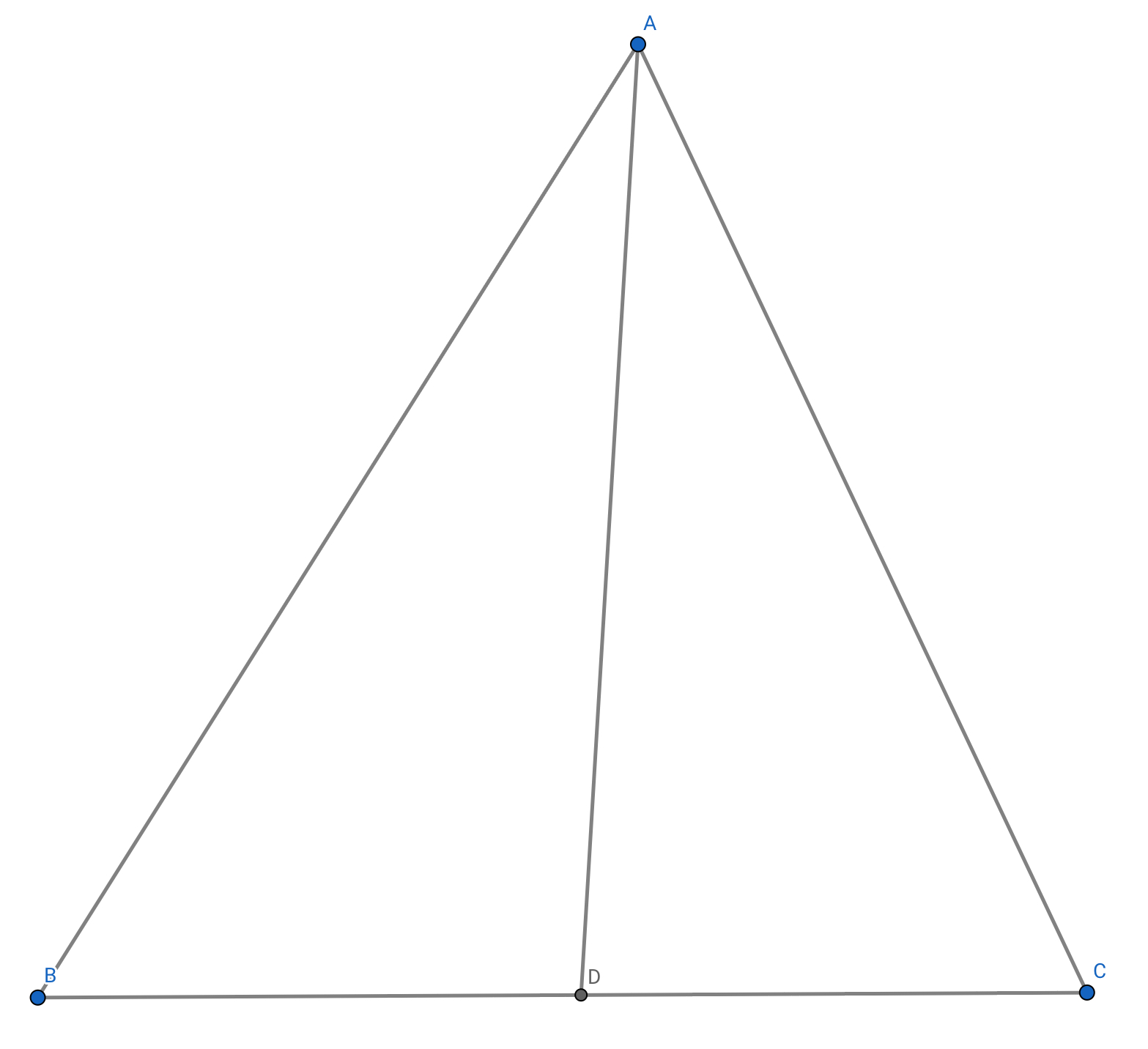
剧场版动画的58分54秒处，出现了主角团参加高考时，猪熊阳子遇到的一道平面几何试题。动画中仅能看到第一个小问的题干。本题为标准的平面几何问题，符合日本高中会考的难度。
|
| 翻译后的题干 | |||
|---|---|---|---|
|
由于题目不全，依题意在GeoGebra中画出图形。
题目：如图。在$Rt\triangle ABC$中，$\angle ACB=90\degree$，AC=3，AB=5。点O是$\triangle ABC$的内心。连结AO并延长，交BC于点L。$\triangle ABC$的一条外角平分线交BC延长线于点M。求LM的长。
注：本题实际为填空题而非解答题。被盖住的下文中，有要求考生补全角平分线定理的提示，以引导考生得出答案。接下来的解答中，会给出定理内容和证明 |
| 基于题目下方提示，还原出的解答 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
本方法基于内角平分线定理与相似三角形的性质。 角平分线定理非书本内容，以下给出详细说明。
根据勾股定理，可知AC2+BC2=AB2，因此BC=4。
根据内角平分线原理，可知ABBL=ACCL，即BL:CL=5:3，因此BL=2.5，CL=1.5。
根据外角平分线性质，可知$\angle LAM=90\degree$，因$\angle C=90\degree$，可知$\triangle LAC\sim \triangle CAM$。
根据相似三角形性质，可知$\frac{LC}{AC}=\frac{AC}{CM}$，即$CM=\frac{3\times 3}{1.5}=6$，因此$LM=LC+CM=1.5+6=7.5$。
|
| 另一种解法 |
|---|
|
本方法仅使用三角形的全等与面积公式，无需任何相似三角形知识。 根据勾股定理，可知$AC^{2}+BC^{2}=AB^{2}$，因此$BC=4$。
从$点L和点M$向射线$BA$作垂线，分别与$BA$交于$点D和点F$。
由角平分线的性质，可知$\triangle ACL\cong \triangle ADL$，以及$\triangle ACM\cong \triangle AFM$。令$DL=CL=x，MC=MF=y$。
在$\triangle ABC$中，由面积等式$\frac{AB\times DL}{2}+\frac{AC\times CL}{2} =S_{\triangle ABL}+S_{\triangle ACL}=S_{\triangle ABC}=\frac{AC\times BC}{2} $，因此$\frac{5x}{2} + \frac{3x}{2} =\frac{3\times 4}{2} $，解得$x=1.5$。
在$\triangle BFM$中，由面积等式$\frac{AC\times B}{2}+\frac{AF\times FM}{2}=S_{\triangle ABM}+S_{\triangle AFM}=S_{\triangle BFM}=\frac{BF\times MF}{2}$，因此$\frac{4+3}{2}y+\frac{3}{2}y=\frac{5+3}{2}y$，可得$y=6$。
由上可知，$LM=CL+CM=x+y=1.5+6=7.5$。
|
J
《寄生兽》
动画第三集14分钟左右，教师田村玲子在黑板上写下了两个对数函数相关的数学题。而在下一个场景中，立川裕子所持的数学教科书中也出现了对应的“对数函数”章节。
|
《寄宿学校的朱丽叶》
第三集
动画第三集13分钟左右，夏尔特琉·威斯提亚在上课时在黑板上推导了大段数学公式，如下图所示：
|
黑板上推导的大量多项式，虽然较为模糊，但根据其极具辨认性的公式形态（根号、三次根号、多项式系数等），可确定其为一元四次方程$ax^{4}+bx^{3}+cx^{2}+dx+e=0$的求根公式。不过一般数学学生们，是不会将整个公式全部写成一大团的，而会将其进行一定的拆分。
不论公式正确与否，一个高中生会完整地推导一元四次方程公式，貌似有点离谱……
| 给数学系强迫症欣赏的一元四次方程公式 |
|---|
|
一元四次方程的一般解公式为 $$x_{1,2}=-\frac{b}{4 a}-S \pm \frac{1}{2} \sqrt{-4 S^{2}-2 p+\frac{q}{S}} $$
$$x_{3,4}=-\frac{b}{4 a}+S \pm \frac{1}{2} \sqrt{-4 S^{2}-2 p-\frac{q}{S}}$$
其中$p$与$q$遵从以下定义：
$$p=\frac{8 a c-3 b^{2}}{8 a^{2}}, q=\frac{b^{3}-4 a b c+8 a^{2} d}{8 a^{3}}$$
而$S$与$Q$的值依赖于判别式：
$$S=\frac{1}{2} \sqrt{-\frac{2}{3} p+\frac{1}{3 a}\left(Q+\frac{\Delta_{0}}{Q}\right)}$$
$$Q=\sqrt[3]{\frac{\Delta_{1}+\sqrt{\Delta_{1}^{2}-4 \Delta_{0}^{3}}}{2}}$$
判别式的定义为：
$$\Delta_{0} =c^{2}-3 b d+12 a e$$
$$\Delta_{1} =2 c^{3}-9 b c d+27 b^{2} e+27 a d^{2}-72 a c e$$
|
第四集
动画第四集5分钟左右，黑犬寮进行考试合训时，狛井莲季在白板上写下了数学模拟卷的部分答案，均为因式分解题型。
动画第四集10分钟左右，狛井莲季的幼时回忆中，出现了犬冢露壬雄在其辅导后，考到90分的数学考卷。其中题型为两位数加减法，符合该回忆中两人均为小学生的设定。
|
K
L
《兰斯系列》
以下内容含有剧透成分，可能影响观赏作品兴趣，请酌情阅读
在《兰斯10 决战》第二部中，主角团（魔王之子）一行人被迫进入迷宫中的裸体结界。女生苏茜诺·甘地在看到男生赞斯·利萨斯的裸体时吓了一跳，小声念叨魔法公式以使自己忘掉，而这个魔法公式实际上是一元二次方程求根公式。
|
《理科生坠入情网，故尝试证明。》
以下内容含有剧透成分，可能影响观赏作品兴趣，请酌情阅读
本作中除数学问题外，也出现了大量理论计算机相关的问题。虽然严格意义上计算机科学相关问题并不在本条目的收录范围中，但鉴于其与组合数学等领域的关联，在此予以保留。
第一集
多项式时间规约
在第一集开头2分钟左右，冰室菖蒲和雪村心夜的交流中，提到了雪村心夜正在撰写关于多项式时间规约的论文。雪村心夜说自己在解法中使用了哈密顿问题，之后被冰室菖蒲吐槽到“借用了理查德·卡尔普的证明”。
多项式时间规约（Polynomial Time Reduction）是理论计算机中常见的方法，用于证明两个问题的计算复杂度相同。理查德·卡尔普是美国著名的理论计算机科学家，他在1972年发布的论文“Reducibility Among Combinatorial Problems”，证明了21个理论计算机问题之间可以进行多项式时间规约（亦即它们的计算复杂度相同，均为NP-Complete），而哈密顿问题为这21个问题之一，因此冰室菖蒲提到的证明确实存在。至于雪村心夜的论文究竟是将哪个问题规约成了哈密顿问题，动画中并未提及。
图灵机
在第一集开头7分钟左右，雪村心夜在研究是否可以构造一个图灵机（Turing Machine），在输入一些观察条件的基础下，来判断“A是否喜欢B”。
图灵机是理论计算机的常见计算模型，它可以用来模拟所有可以用电脑计算的算法。因此雪村心夜提出的问题，虽然听上去很高级，但本质即为是否可以用一个确定的算法来判断“A是否喜欢B”。至于这个问题是否有意义就是另一件事了……
归无假设
第一集14分钟开始，在本集的理科熊科普时间中，介绍了归无假设（Null Hypothesis）这一统计概念，下列内容直接使用了原视频中的解释。
归无假设是指统计学中，「把想要证明的事物回归于无」的假设。简单来说，如果我们建立一个假设，然后发现在现有的数据下，其发生概率很低（小于5%），我们就可以认为该假设是错误的（即驳斥该假设）。通过这样的方法，我们可以在统计上，严谨地排除一些猜想发生的可能性。
动画中举的例子为，假如我们想要证明“乌鸦是黑色的”。即使我们连续看到了100只黑色的乌鸦，在统计上我们不能直接否定没有其他颜色的乌鸦。但我们可以作以下的归无假设：
- 归无假设1: “有50%的乌鸦是黑色的，另外50%的乌鸦是彩色的”，在这一假设下，连续看到了100只黑色的乌鸦的概率为$$(50\%)^{100}\approx 7.88\times 10^{-31}$$
- 理科熊吐槽了这种概率比被陨石砸中一兆次还低。此时我们就可以驳斥这一假设。
- 归无假设2: “有90%的乌鸦是黑色的，另外10%的乌鸦是彩色的”，在这一假设下，连续看到了100只黑色的乌鸦的概率为$$(90\%)^{100}\approx 0.00265\%$$
- 这个概率依然很低，因此我们还是可以驳斥这一假设。
- 归无假设3: “有97.1%的乌鸦是黑色的，另外2.9%的乌鸦是彩色的”，在这一假设下，连续看到了100只黑色的乌鸦的概率为$$(97.1\%)^{100}\approx 5.27\%$$
- 这时概率超过了5%，只有在这类情况下，我们才会认为这一假设可能发生。
当然以上概率计算成立的前提条件是，我们想要研究的事件是互相独立的。同集中冰室菖蒲和雪村心夜将理论运用在连续壁咚的心率提升上，就是一个绝佳的反例：随着壁咚次数的增加，后续壁咚引发的心率变化会逐渐变低，即这些事件并非互相独立。
|
斐波那契数与花瓣
本集16分钟的过场动画中，出现了冰室菖蒲坐在花园中的场景，其中的花瓣标记了数字5、8、13，它们均为斐波那契数。现实中，确实有许多花的常见花瓣数，为斐波那契数列中的数值（3、5、8、13、21、34、55），其背后的理由尚待人类考究。
|
汉诺塔问题
本集19分钟左右，奏言叶在讲到自己选择理科的故事中，提到自己高中时用递归的方法解决了汉诺塔问题，并计算出其所需步数为$2^n-1$。
汉诺塔问题是源于印度传说的一个数学问题。问题叙述如下：有三根编号为$A、B、C$的杆，在$A$杆自上而下、由小到大按顺序穿着$n$个圆盘。目标是把$A$杆上的圆盘，全部移到$C$杆上，在移动过程中需要确保三根杆上均为大盘在下，小盘在上，一次只能移动一个圆盘。求该过程的所需最少步数。
| 动画中未给出的，汉诺塔问题的递归解法 |
|---|
|
|
维恩图
本集20分钟左右，雪村心夜将不同人恋爱的条件分别抽象化成了集合，并画出了对应的维恩图，希望通过研究交集的形式来证明恋爱的基本条件。但由于不同人喜欢的条件可能并不相同，该交集大概率为空集……
|
《莉兹与青鸟》
本电影中最完整的题目出现于结尾处伞木希美的大学入学考试书籍中。题目如下：
- 已知自然数$x, y$互质，求证$x+y$与$x \times y$互质。
| 伞木希美的证法 |
|---|
| 其他证法 |
|---|
|
因为$(x, y)=1$，所以$(x, x+y)=1$，所以$(x \times y, x+y)=1$。 |
虽然作为一道数学题，本题和其他题目相比非常基础，但值得一提的是，质数是电影中一个频繁出现的元素：据青学家研究，电影特写中的物体个数均为质数，乃至希美和霙二人的脚步频率也是由一开始的互质到最后的不互质[2]。此外，本电影开头结尾出现的单词 disjoint 也是数学术语，即“不相交”；据访谈，结尾处的色块相交实际上指的是文氏图。
M
《魔法少女小圆》
数学问题
第一集以及第十集轮回中，晓美焰在白板上求解的几道数学题，包括了中学代数与数论的题型。需要注意的是，番剧设定为初中生，而这些题目明显超出了一般初中课本范围。所以大概也只有轮回过无数次的小焰知道怎么做。
|
| 题目 |
|---|
|
（1）求不定方程$a^{3}+a^{2}-1=(a-1)b$的所有整数解$(a, b)$。
（2）已知$f(x)=\frac{4x+\sqrt{4x^{2}-1}}{\sqrt{2x+1}+\sqrt{2x-1}}$，求$f(1)+f(2)+f(3)+\cdots+f(60)$的值。
（3）已知$x, a, b$为整数，$a$除以14的余数为6，$b$除以14的余数为1，且$x^{2}-2ax+b=0$有整数解，求$x$除以14的余数。
（4）已知$p$为素数，$n$为任意自然数，证明$(1+n)^{p}-n^{p}-1$能被$p$整除。
|
官方解法及评注
以下解法摘自番剧中晓美焰的解法。
| 题（1）解法 |
|---|
|
若$b\geq 1$，则可将右式移到左侧，并因式分解可知$$\begin{aligned} &(a^{3}+a^{2}-1)-(a-1)b\\&=(a^{3}-1)+(a^{2}-1)+1-(a-1)b\\&=(a-1)(a^{2}+a+1)+(a-1)(a+1)+1-(a-1)b\\&=(a-1)(a^{2}+2a-b+2)+1=0\end{aligned}$$
因此$(a-1)(a^{2}+2a-b+2)=-1$，即$a-1=1$或$a-1=-1$。
情况1:若$a-1=1$，则$a=2$，代入$a^{2}+2a-b+2=-1$可知$b=11$
情况2:若$a-1=-1$，则$a=0$，代入$a^{2}+2a-b+2=1$可知$b=1$
因此所有解为$(a, b)=(0,1), (2, 11)$
|
| 题（2）解法 |
|---|
|
令$a_{n}=\sqrt{2n-1}$，则$$\begin{aligned} &a_{n+1}a_{n}=\sqrt{2n+1}\sqrt{2n-1}=\sqrt{4n^{2}-1}, \\&a_{n+1}^{2}+a_{n}^{2}=(\sqrt{2n+1})^{2}+(\sqrt{2n-1})^{2}=4n, \\&a_{n+1}^{2}-a_{n}^{2}=(\sqrt{2n+1})^{2}-(\sqrt{2n-1})^{2}=2\end{aligned}$$
因此可知$$\begin{aligned}&f(n)=\frac{4n+\sqrt{4n^{2}-1}}{\sqrt{2n+1}+\sqrt{2n-1}}\\&=\frac{a_{n+1}^{2}+a_{n+1}a_{n}+a_{n}^{2}}{a_{n+1}+a_{n}}\\&=\frac{(a_{n+1}-a_{n})(a_{n+1}^{2}+a_{n+1}a_{n}+a_{n}^{2})}{(a_{n+1}-a_{n})(a_{n+1}+a_{n})}\end{aligned}$$
注意番剧中晓美焰写的平方记号很小，因此$a_{n}^{2}$写的很像$a_{n^{2}}$，但学习过数学的读者应该能明白她的本意 （以上为番剧中显示的答案部分，之后的证明未在番剧上显示，下为参考思路） $$\begin{aligned}&f(n)=\frac{(a_{n+1}-a_{n})(a_{n+1}^{2}+a_{n+1}a_{n}+a_{n}^{2})}{(a_{n+1}-a_{n})(a_{n+1}+a_{n})}\\&=\frac{a_{n+1}^{3}-a_{n}^{3}}{a_{n+1}^{2}-a_{n}^{2}}\\&=\frac{1}{2}(a_{n+1}^{3}-a_{n}^{3})\end{aligned}$$
$$\begin{aligned}&f(1)+f(2)+f(3)+\cdots+f(60)\\&=\frac{1}{2}[(a_{2}^{3}-a_{1}^{3})+(a_{3}^{3}-a_{2}^{3})+\cdots+(a_{61}^{3}-a_{60}^{3})]\\&=\frac{1}{2}(a_{61}^{3}-a_{1}^{3})\\&=\frac{1}{2}((\sqrt{121})^{3}-(\sqrt{1})^{3})=665\end{aligned}$$
|
| 题（3）解法 |
|---|
|
令$x=14q+r, a=14s+6, b=14t+1$，则二次方程的左侧可简化为$$\begin{aligned}&x^{2}-2ax+b\\&=(14q+r)^{2}-2(14s+6)(14q+r)+(14t+1)\\&=14(14q^{2}+2qr-28qs-2rs-12q+t-r)+(r+1)^{2}=0\end{aligned}$$因此可知14整除$(r+1)^{2}$。因为$14=2\times 7$为两个素数之积，可知14整除$r+1$，即$r$除以14的余数为13。
|
| 题（4）解法 |
|---|
|
令$_mC_k$代表从m个物品中选择k个的组合数（不同国家组合数的写法不同，此记号为日本使用）。根据二项式定理可知$$\begin{aligned}&(1+n)^{m}\\&=_mC_0+_mC_1 n+\cdots+_mC_{m-1} n^{m-1}+_mC_{m} n^{m}\end{aligned}$$根据组合性质，可知$$\begin{aligned}&k_pC_k=k\frac{p!}{k!(p-k)!}\\&=p\frac{(p-1)!}{(k-1)!(p-k)!}=p _{p-1}C_{k-1}\end{aligned}$$因此对于$1\leq k\leq p-1$，$_pC_k$能被$p$整除
（下列内容被正在写字的晓美焰挡住了，为非官方解答） 将上述内容代入本问题可知$$\begin{aligned}&(1+n)^{p}-n^{p}-1\\&=_pC_1 n+_pC_2 n^{2}+\cdots+_pC_{p-1} n^{p-1}\end{aligned}$$右式每一项都能被$p$整除，因此左式也能被$p$整除，证毕。
|
N
O
《One Room》
本番中，教数学的题材出现在了两个不同的故事中，注意两个故事的主人公设定并不相同。前一个是教学妹的学霸，后一个是被大姐姐教的学渣。
花坂结衣篇
第1季第2集开头，主人公教花坂结衣数学时，作业本上出现了数学题与解答过程。因内容较模糊，无法看出太多细节。不过可以确认的是，记载的数学内容为标准的高中内容，符合本番设定中花坂结衣参加高校入学测试的难度。
|
| 根据图片还原出的部分题目 |
|---|
|
左上方题目本： （1）左侧页面疑似为一道解析几何题（可辨认出含有原点O等坐标系要素），题目内容为求一个与p、q两参数相关的三角形OPQ的面积，并在特定条件下求解该面积的最大值。然而在没有图片的情况下，无法看出具体P、Q两点的构造方式。
（2）右侧页面为一道概率问题，内容大致意思为“令n次中发生k次，随机变量$X=k$的概率p。请用n与k表示p，并求出p的最大值”。与之最相近的数学题可能为“投掷n次硬币，求k次向上概率，并寻找该概率的最大值”，但在没有看明白全题之前也无法判断原题。
右下方作业本： （3）作业本上的内容大致为一道代数大题：“求解含有变量a的三次函数f(x)在某定义域上的最大值M(a)，并对a的不同情况进行讨论”（可隐约看到解法和图形中，有标记与计算导数为零的点和定义域两侧端点的值，因而推断题型为此）。
|
织崎纱耶篇
第3集第8集中，织崎纱耶帮助主人公复习数学时，亦出现了写满数学解答的作业本。虽然题干并没有在番剧中给出，但可以推断出是一道几何与三角函数结合的大题，符合日本高中难度。
- 作业本中的绿色批注，大概率是织崎纱耶为主人公标出的关键概念/步骤。
- 剧中织崎纱耶对主人公的评价是“思路大致是正确的，但是容易粗心写错答案”，但在作业本中，除了一道题的中间步骤存在小错误以外，并未有写错答案的情况。
可猜测作业本中的内容，并非主人公真正答题时的内容，而是织崎纱耶教导后，主人公重做后的解答。
|
| 根据解答，还原出的题干 |
|---|
|
在作业本左侧图片所示的平面直角坐标系中，各坐标点满足条件$OA=OB=1$，$\angle OBP=\angle BAQ=x$。
（1）证明：$\triangle PRA\sim\triangle PAB$。
（2）求$AP$的长度，用$x$进行表示。
（3）求$\triangle ABR$的最大面积。
|
下列解答基于作业本上的做法，为保证证明通顺，有一定修正。红色内容在作业本上被遮挡，为非官方解答。
| 第一问解答 |
|---|
|
由于$\angle APR=\angle APB$（同一个角），且$\angle RAP=\angle ABP=45\degree - x$，因此$\triangle PRA$和$\triangle PAB$的三个角均相等，因此它们相似。
|
| 第二问解答 |
|---|
|
根据第一问的结论，以及相似三角形的性质，可知$AR:AB=PA:PB$
$$\begin{aligned}AR&=\frac{AB\cdot PA}{PB}\\&=\frac{AB\cdot(OA-OP)}{PB}\\&=\frac{\sqrt{2}(1-\tan x)}{1/\cos x}\\&=\sqrt{2}(1-\tan x)\cos x\end{aligned}$$
|
| 第三问解法1（不使用第二问结论） |
|---|
|
将$\triangle ABR$沿着边$AB$对称翻转，令$R$的对称点为$R'$。
则$R'$必定在以$O$为圆心，半径为1的圆弧上。（作业本上画的圆弧，本质便是使用了这个特性。对于为何这点在圆弧上，不确定的读者，可以计算一下对应的圆周角。）
现在，考虑三角形$\triangle OAR'$与$\triangle OBR'$在底边$\triangle OR'$上的高度总和。由于$OR'$和$AB$的夹角为$2x+\frac{\pi}{4}$，因此总高度为$\frac{\sqrt{2}}{2}\sin\left(2x+\frac{\pi}{4}\right)$
因此，三角形的ABR的面积为$$\begin{aligned}&\triangle OBR'+\triangle OAR'-\triangle OAB\\&=\frac{\sqrt{2}}{2}\sin\left(2x+\frac{\pi}{4}\right)-\frac{1}{2}\end{aligned}$$
由于$0\leq x\leq \frac{\pi}{4}$，根据$\sin$函数的性质，最大值在$x=\frac{\pi}{8}$取到，为$\frac{\sqrt{2}-1}{2}$。
|
| 第三问解法2（使用第二问结论） |
|---|
|
根据第二问中求得的$AR$长度，由三角形的面积公式、以及三角函数的二倍角公式，可知$$\begin{aligned}\triangle ABR &=\frac{1}{2}AB\cdot AR\cdot \sin\angle BAR\\&=\frac{1}{2}\cdot \sqrt{2}\cdot \sqrt{2}(1-\tan x)\cos x\cdot \sin x\\&=\sin x\cos x-\sin^{2} x\\&=\frac{1}{2}\sin (2x)+\frac{1}{2}\cos(2x)-\frac{1}{2}\end{aligned}$$
我们可以进一步对上面的式子，使用余弦和角公式可得$$\begin{aligned}&\frac{1}{2}\sin (2x)+\frac{1}{2}\cos(2x)-\frac{1}{2}\\&=\frac{\sqrt{2}}{2}\left(\frac{1}{\sqrt{2}}\sin (2x)+\frac{1}{\sqrt{2}}\cos(2x)\right)-\frac{1}{2}\\&=\frac{\sqrt{2}}{2}\left(\sin(\frac{\pi}{4})\sin (2x)+\cos(\frac{\pi}{4})\cos(2x)\right)-\frac{1}{2}\\&=\frac{\sqrt{2}}{2}\cos\left(2x-\frac{\pi}{4}\right)-\frac{1}{2}\end{aligned}$$
（上面式子第二行的首项$\frac{\sqrt{2}}{2}$，在动画原图中误写成了$\frac{1}{2}$，织崎纱耶后续的在笔记本上指出错误的剧情，大概率也是针对这一点。）
由于$0\leq x\leq \frac{\pi}{4}$，根据$\cos$函数的性质，上述面积的最大值于$x=\frac{\pi}{8}$取到，为$\frac{\sqrt{2}-1}{2}$。
|
P
Q
《轻音少女》
在第1季第3集，轻音部一行来到平泽唯家中帮助平泽唯补习功课时，秋山澪曾给平泽唯讲解了一道因式分解的题目：
$x^2-xy-6y^2+2x-y+1$
不过，由于平泽唯很快就被讲解声所催眠了，本剧并没有将秋山澪的解法解释完毕。
| 非官方解法 |
|---|
|
$$\begin{aligned}原式&=(x^2+2x+1)-y(x+1)-6y^2\\&=(x+1)^2-y(x+1)-6y^2.\end{aligned}$$
令$z=x+1,$
则原式$=z^2-yz-6y^2.$
使用十字相乘法可得 $$\begin{aligned}原式&=(z-3y)(z+2y)\\&=(x-3y+1)(x+2y+1).\end{aligned}$$
|
|
R
S
《Slow Start》
第六集中万年大会帮助几位主角辅导功课时，使用了一本微积分课本。万年大会作为高中毕业学生，学过微积分并无不妥。但主角团作为一般高中生，高一刚入校就上微积分，似乎有些超前。建议请数学老师出来解释一下。
- 课本左侧页面包含多道求切线和法线的问题，以及参数方程求导的问题。
- 课本右侧页面则包含下列三角函数的经典积分递归公式（但三个公式中有两个写错了）。
| 正确的积分递归公式及说明 |
|---|
|
$$（1）\int\limits \sin^{n}xdx=-\frac{1}{n}\sin^{n-1}x\cos x+\frac{n-1}{n}\int \sin^{n-2}xdx$$ $$（2）\int\limits \cos^{n}xdx=\frac{1}{n}\cos^{n-1}x\sin x+\frac{n-1}{n}\int \cos^{n-2}xdx$$ $$（3）\int\limits \tan^{n}xdx=\frac{1}{n-1}\tan^{n-1}x-\int \tan^{n-2}xdx$$
番剧中公式（1）的左侧错写成了$\int\limits \sin^{2}xdx$，右侧的第一项遗漏了负号；公式（3）的右侧第一项分数被错写成了$\frac{1}{n}$。
|
|
T
U
V
W
X
Y
《一周的朋友。》
第一集
在动画第一集的20:45左右，女主藤宫香织课桌上的数学书中，可发现一些三角函数例题和习题。
|
| 上方三小题 |
|---|
|
求下列三个三角函数的值。 (1) $\sin 30\degree$
(2) $\cos 105\degree$
(3) $\tan 75\degree$
|
| 非官方解答 |
|---|
|
三角函数基础题，直接计算或使用和角公式即可解决。 (1) $$\sin 30\degree=\frac{1}{2}.$$
(2) $$\begin{aligned}\cos 105\degree&=\cos (45\degree + 60\degree)=\cos 45\degree \cos 60\degree-\sin 45\degree \sin 60\degree\\ &=\frac{\sqrt{2}}{2}\times\frac{1}{2}-\frac{\sqrt{2}}{2}\times\frac{\sqrt{3}}{2}=\frac{\sqrt{2}-\sqrt{6}}{4}.\end{aligned}$$
(3) $$\begin{aligned}\tan 75\degree&=\tan (30\degree +45\degree)=\frac{\tan 30\degree+\tan 45\degree}{1-\tan 30\degree \tan 45\degree}\\
&=\frac{\frac{\sqrt{3}}{3}+1}{1-\frac{\sqrt{3}}{3}\times 1}=\sqrt{3}+2.\end{aligned}$$
|
| 中间例题和课本的解答 |
|---|
|
题目: 证明 $$\sin(\alpha+\beta)\sin(\alpha-\beta)=\sin^2 \alpha-\sin^2 \beta.$$
证明: $$\begin{aligned}左边 &=(\sin \alpha \cos \beta + \cos \alpha \sin \beta)(\sin \alpha \cos \beta - \cos \alpha \sin \beta) \\
&=\sin^2\alpha \cos^2\beta-\cos^2\alpha \sin^2\beta \\
&=\sin^2\alpha(1-\sin^2\beta)-(1-\sin^2\alpha)\sin^2\beta \\
&=\sin^2\alpha-\sin^2\alpha \sin^2\beta-\sin^2\beta+\sin^2\alpha \sin^2\beta \\
&=\sin^2\alpha-\sin^2\beta=右边.
\end{aligned}$$
|
| 下方习题 |
|---|
|
证明: $$\cos(\alpha+\beta)\cos(\alpha-\beta)=\cos^2 \alpha-\cos^2 \beta=\cos^2 \beta-\cos^2 \alpha.$$
|
| 非官方解答 |
|---|
|
证明:先证左边与中间相等 $$\begin{aligned}左边&=(\cos \alpha \cos \beta - \sin \alpha \sin \beta)(\cos \alpha \cos \beta + \sin \alpha \sin \beta) \\
&=\cos^2\alpha \cos^2\beta-\sin^2\alpha \sin^2\beta \\
&=\cos^2\alpha(1-\cos^2\beta)-(1-\cos^2\alpha)\sin^2\beta \\
&=\cos^2\alpha-\cos^2\alpha \cos^2\beta-\sin^2\beta+\cos^2\alpha \sin^2\beta \\
&=\cos^2\alpha-\sin^2\beta=中间.
\end{aligned}$$
证完左边和中间相等,不难证明左边和右边相等,方法相同. $$\begin{aligned}左边&=(\cos \alpha \cos \beta - \sin \alpha \sin \beta)(\cos \alpha \cos \beta + \sin \alpha \sin \beta) \\
&=\cos^2\alpha \cos^2\beta-\sin^2\alpha \sin^2\beta \\
&=(1-\sin^2\alpha)\cos^2\beta-\sin^2\alpha(1-\cos^2\beta) \\
&=\cos^2\beta-\sin^2\alpha \cos^2\beta -\sin^2\alpha+\sin^2\alpha \cos^2\beta \\
&=\cos^2\beta-\sin^2\alpha=右边.
\end{aligned}$$
|
第三集
第三集18:49左右，黑板上出现了一道三角函数求值题。
|
| 题目 |
|---|
|
当$\tan \theta=\frac{1}{2}$时，试求$$P=\frac{18 \sin \theta \cos \theta - 9 \cos \theta}{1 - \sin \theta + \sin^2 \theta - \cos^2 \theta}$$的值.
|
| 藤宫香织的解答 |
|---|
|
$$\begin{aligned}P&= \frac{9 ( 2 \sin \theta \cos \theta - \cos \theta )}{1 - \sin \theta + \sin^2 \theta - \cos^2 \theta}\\
&= \frac{9 \cos \theta ( 2 \sin \theta - 1 )}{\sin^2 \theta - \sin \theta + \sin^2 \theta}\\\end{aligned}$$
$$\begin{aligned}&= \frac{9 \cos \theta ( 2 \sin \theta - 1 )}{1 - \cos^2 \theta - \sin \theta + \sin^2 \theta}\end{aligned}$$ $$\begin{aligned}&= \frac{9 \cos \theta ( 2 \sin \theta - 1 )}{\sin \theta ( 2 \sin \theta - 1 )}\\ &= 9 \times \frac{\cos \theta}{\sin \theta}\\ &= 9 \times \frac{1}{\tan \theta}.\end{aligned}$$将$\tan \theta = \frac{1}{2}$代入,得$P = 9 \times \frac{1}{\frac{1}{2}} = 18$.
红色部分疑似解答重复。 顺带一提，18对男女主有着特殊含义。如果爱情有质量，那一定是18g！ |
Z
特殊作品名
| |||||||||||||||||||||||||||||||||
参考资料
外部链接
数学相关番剧盘点向视频1：https://www.bilibili.com/video/av89059513
数学相关番剧盘点向视频2：https://www.bilibili.com/video/BV1SE411j7kP
外网上对数学相关番剧的盘点（日文）：https://www.anikore.jp/tag/%E6%95%B0%E5%AD%A6/